Inscribed angle and central angle worksheet – Embark on an exploration of inscribed and central angles with our captivating worksheet. This comprehensive resource delves into the intricacies of these angles, their properties, and their applications. Prepare to deepen your understanding and master the concepts that underpin this fascinating mathematical realm.
Within this worksheet, you will encounter a wealth of knowledge and practical exercises that will illuminate the relationship between inscribed and central angles, empowering you to tackle complex problems with confidence.
Inscribed Angles and Central Angles: Inscribed Angle And Central Angle Worksheet
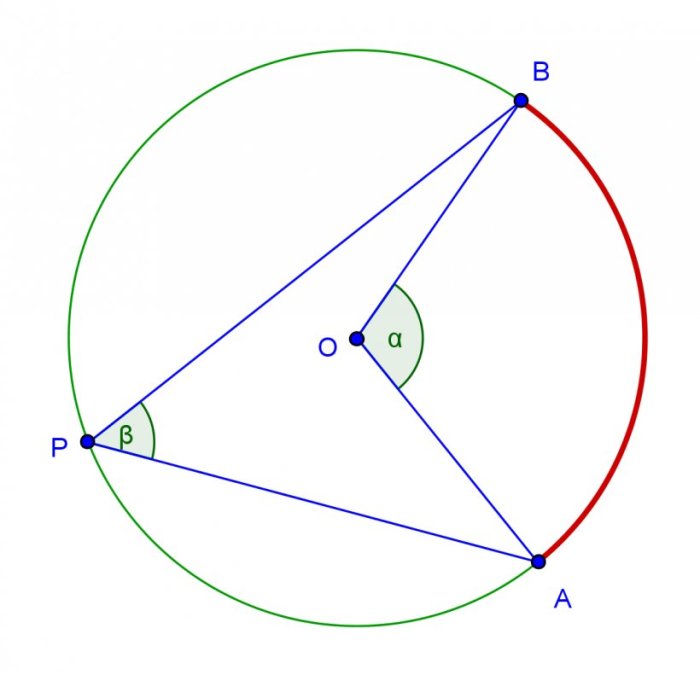
In geometry, inscribed angles and central angles are two types of angles that are formed within a circle. Inscribed angles are formed by two chords that intersect inside the circle, while central angles are formed by two radii that intersect at the center of the circle.
Relationship between Inscribed and Central Angles
The measure of an inscribed angle is half the measure of its corresponding central angle. This relationship can be expressed mathematically as follows:
m∠Inscribed = 1/2 m∠Central
Types of Inscribed Angles, Inscribed angle and central angle worksheet
Inscribed angles can be classified into three types based on their position in the circle:
- Acute inscribed angles:Angles less than 90 degrees.
- Right inscribed angles:Angles equal to 90 degrees.
- Obtuse inscribed angles:Angles greater than 90 degrees.
Properties of Inscribed Angles
Inscribed angles have several important properties:
- They are always less than 180 degrees.
- They are opposite to equal central angles.
- They are equal to half the sum of the intercepted arcs.
Worksheet Design
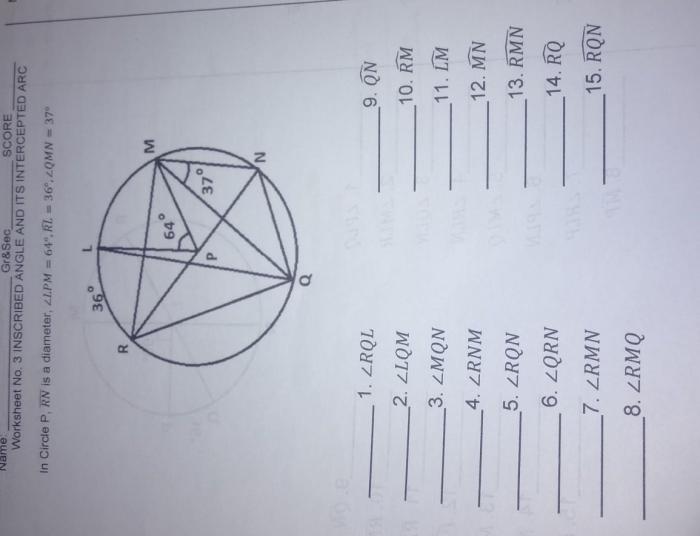
The worksheet should include various problems related to inscribed angles and central angles. The problems can be categorized into the following types:
- Finding the measure of an inscribed angle given the measure of its corresponding central angle.
- Finding the measure of a central angle given the measure of its corresponding inscribed angle.
- Determining the type of inscribed angle based on its position in the circle.
- Solving problems involving the properties of inscribed angles.
Essential FAQs
What is the relationship between an inscribed angle and its corresponding central angle?
The measure of an inscribed angle is half the measure of its corresponding central angle.
How can I use the properties of inscribed angles to solve problems?
By understanding the relationship between inscribed angles and chords, tangents, and diameters, you can use their properties to determine unknown angle measures and solve geometric problems.