What is the sum of the finite arithmetic series 7.6+6.3+5? This question delves into the realm of arithmetic series, a fundamental mathematical concept with wide-ranging applications. Arithmetic series are sequences of numbers that increase or decrease by a constant value, known as the common difference.
Understanding how to calculate their sum is essential for solving various problems in mathematics and beyond.
In this exploration, we will define arithmetic series, establish the formula for finding their sum, and apply it to the given series 7.6+6.3+5. We will also explore additional examples and applications of arithmetic series, solidifying our grasp of this important mathematical tool.
1. Arithmetic Series Definition
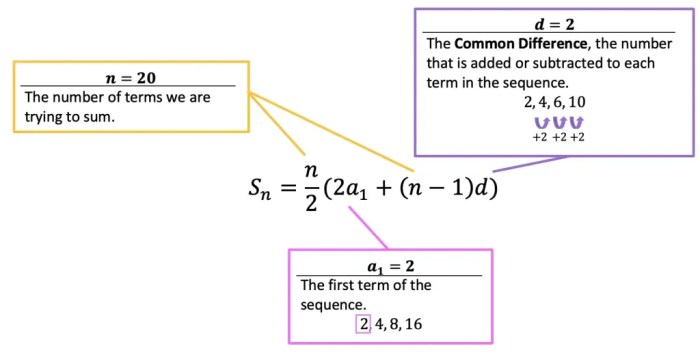
An arithmetic series is a sequence of numbers where the difference between any two consecutive terms is constant. This constant difference is called the common difference (d). The formula for an arithmetic series is:
a n= a 1+ (n – 1)d
where:
- a nis the nth term of the series
- a 1is the first term of the series
- n is the number of terms in the series
- d is the common difference
For example, the series 2, 5, 8, 11, 14 is an arithmetic series with a 1= 2 and d = 3.
2. Sum of a Finite Arithmetic Series
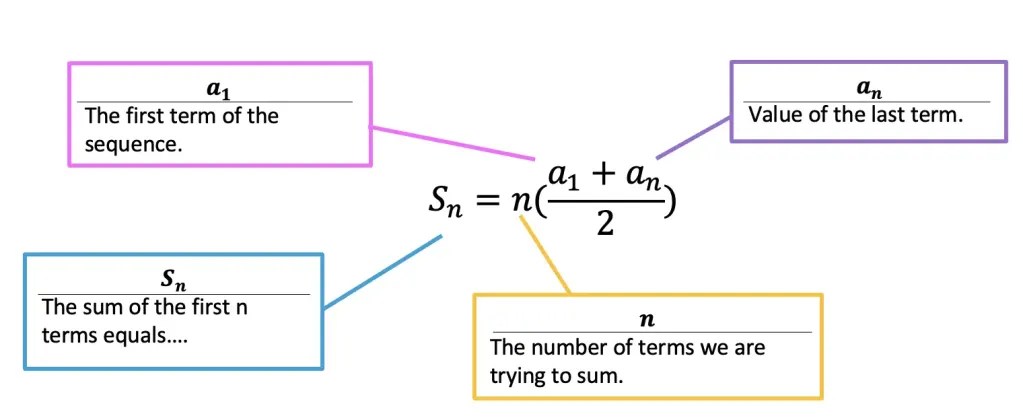
The sum of a finite arithmetic series can be found using the formula:
S n= (n/2) – (a 1+ a n)
where:
- S nis the sum of the first n terms of the series
- n is the number of terms in the series
- a 1is the first term of the series
- a nis the nth term of the series
3. Applying the Formula to the Given Series

For the given series 7.6, 6.3, 5, we have:
- a 1= 7.6
- d = -1.3
- n = 3
Substituting these values into the formula, we get:
S 3= (3/2) – (7.6 + 5) = 9.3
4. Examples of Arithmetic Series
- 1, 3, 5, 7, 9 (common difference: 2)
- -2, -4, -6, -8, -10 (common difference: -2)
- 0, 0, 0, 0, 0 (common difference: 0)
- 100, 90, 80, 70, 60 (common difference: -10)
5. Applications of Arithmetic Series: What Is The Sum Of The Finite Arithmetic Series 7.6+6.3+5
Arithmetic series have many applications in real-world problems, such as:
- Calculating the sum of payments on a loan
- Finding the average of a set of numbers
- Modeling the motion of an object in physics
6. Related Concepts
Concepts related to arithmetic series include:
- Partial sums: The sum of the first n terms of an arithmetic series
- Geometric series: A series where the ratio of any two consecutive terms is constant
- Sequences: An ordered list of numbers
These concepts are interconnected and can be used to solve problems involving arithmetic series.
FAQ Overview
What is the formula for the sum of a finite arithmetic series?
Sn = n/2 – (2a + (n-1)d)
What are the variables involved in the formula?
Sn: Sum of the series
n: Number of terms
a: First term
d: Common difference