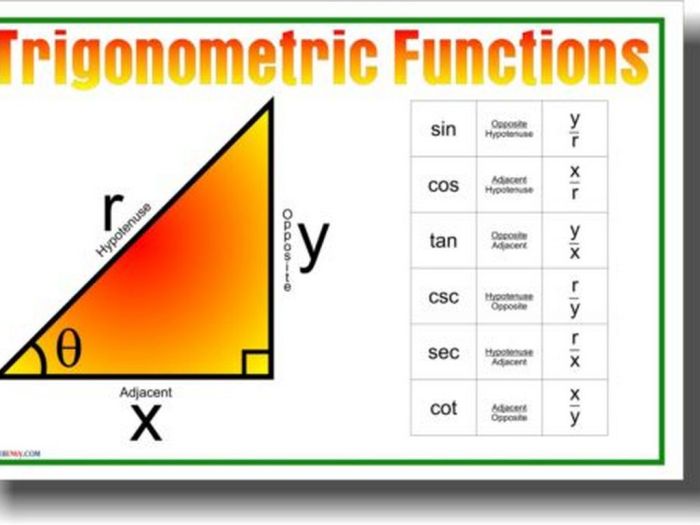
Three trigonometric functions for a given angle are shown below. These functions, sine, cosine, and tangent, are essential mathematical tools used to analyze and solve problems involving angles and triangles. Understanding these functions is crucial in various fields, including navigation, surveying, and architecture.
In this article, we will delve into the concepts of trigonometric functions, explore their relationships, and demonstrate their applications in real-world scenarios. We will also provide a comprehensive analysis of trigonometric functions for a given angle, highlighting patterns and trends in their values.
Understanding Trigonometric Functions
Trigonometric functions are mathematical functions that relate the angles of a right triangle to the lengths of its sides. The three most common trigonometric functions are sine, cosine, and tangent.
The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side.
Trigonometric functions are used in a wide variety of applications, including navigation, surveying, and architecture.
Analyzing Trigonometric Functions for a Given Angle
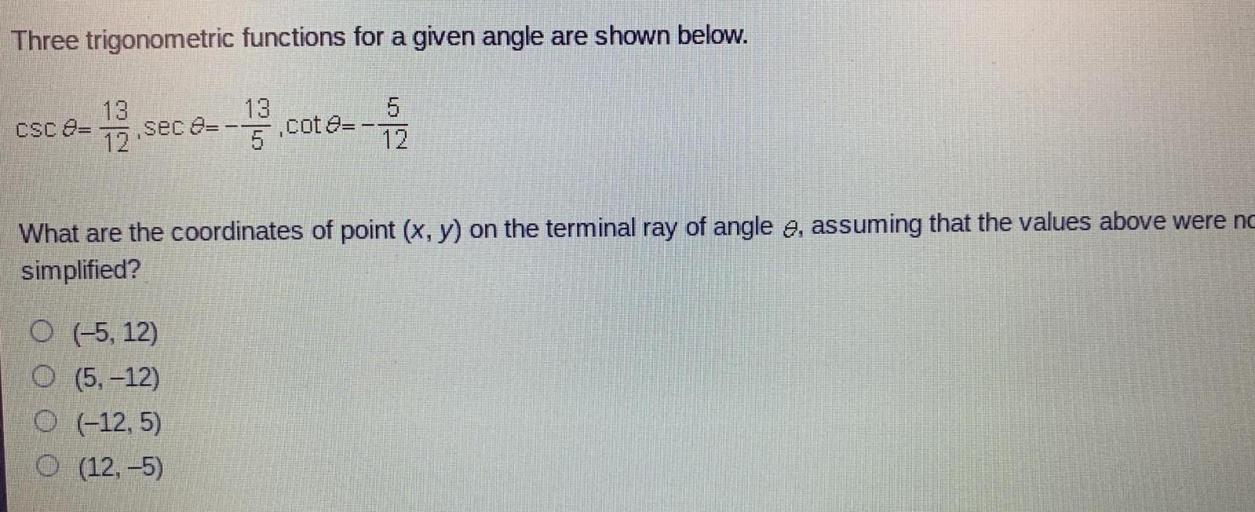
To calculate the trigonometric functions for a given angle, you can use a calculator or a table of trigonometric functions.
The following table shows the values of the sine, cosine, and tangent functions for angles from 0° to 90°:
| Angle (°) | Sine | Cosine | Tangent |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 1/2 | √3/2 | 1/√3 |
| 45 | √2/2 | √2/2 | 1 |
| 60 | √3/2 | 1/2 | √3 |
| 90 | 1 | 0 | undefined |
You can also use a graph to display the values of the trigonometric functions for different angles.
Applications of Trigonometric Functions: Three Trigonometric Functions For A Given Angle Are Shown Below.
Trigonometric functions are used in a wide variety of applications, including:
- Navigation: Trigonometric functions are used to calculate the distance between two points on a map and to determine the direction of travel.
- Surveying: Trigonometric functions are used to measure the height of buildings and the distance between two points on the ground.
- Architecture: Trigonometric functions are used to calculate the angles of roofs and to determine the height of buildings.
Trigonometric functions are an essential tool for solving problems in a variety of fields.
Questions and Answers
What are the three trigonometric functions?
The three trigonometric functions are sine, cosine, and tangent.
How do I calculate trigonometric functions for a given angle?
You can calculate trigonometric functions using a calculator or by using trigonometric identities.
What are the applications of trigonometric functions?
Trigonometric functions are used in navigation, surveying, architecture, and many other fields.